Wärmepumpen Kreisprozess

Clausius Rankine Kreisprozess - der ideale Kreisprozess

Der Clausius Rankine Kreisprozess ist ein thermodynamischer Kreisprozess der u.a. für das Dampfkraftwerk als Vergleichsprozess dient. Er basiert darauf, dass ein Arbeitsmittel in einem geschlossenen Kreislauf zwei mal seinen Aggregatszustand ändert, von flüssig zu gasförmig und wieder zurück. Sein Wirkungsgrad kann den des Carnot Kreisprozesses nicht übertreffen.

Der linkslaufende (entgegengesetzte Richtung) Clausius Rankine Kreisprozess beschreibt die Vorgänge in der idealen Wärmepumpe oder Kältemaschine.

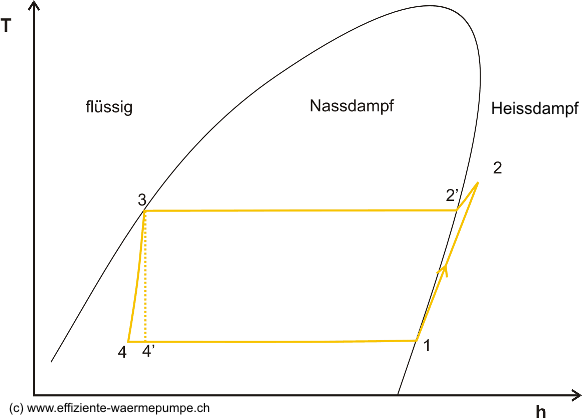
Bild 1: Der ideale Wärmepumpen Kreisprozess

Die 4 Zustandsänderungen sind wie folgt (vgl. Bild 1):

4-1: Isotherme und isobare Verdampfung des Arbeitsmittels im Verdampfer und Wärmeaufnahme auf tiefem Druck- und Temperaturniveau.
1-2: Adiabate Kompression durch den Verdichter und dabei wird Arbeit am System verrichtet.
2-3: Isobare Abkühlung, Kondensation und Unterkühlung des Arbeitsmittels auf hohem Druck- und Temperaturniveau und Wärmeabgabe.
3-4’: Expansion des flüssigen Arbeitsmittels wobei eine teilweise Verdampfung erfolgt. Um einem linksläufigen Clausius Rankine Prozess zu entsprechen müsste dieser Vorgang adiabat vonstatten gehen, also z.B. über eine Turbine erfolgen. Aus Gründen eines vereinfachten Aufbaus und weil der Energieertrag gering ist, wird irreversibel über eine Drossel entspannt bei konstanter Enthalpie (3-4).

Der reale Wärmepumpen Kreisprozess

Im realen Kreisprozess treten verschiedene Nichtidealitäten auf, die den Wirkungsgrad verschlechtern. Der augenfälligste Unterschied ist die Überhitzung des Arbeitsmittels nach dem Verdampfer (Bild 2, 5-1). Dies ist nötig, damit sichergestellt wird, dass das Arbeitsmittel vollständig verdampft und keine Flüssigkeitströpfchen in den Verdichter gelangen und ihn beschädigen. Zudem treten an verschiedenen Stellen Verluste auf.

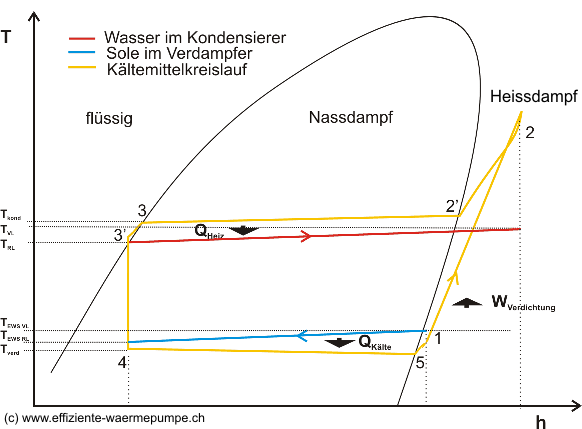
Bild 2: Der reale Wärmepumpen Kreisprozess

Der reale Kreisprozess läuft wie folgt ab (vgl. Bild 2):

4-5: Verdampfung des Arbeitsmittels im Verdampfer. Reibung führt zu Druckabfall und damit zu einer Abnahme der Verdampfungstemperatur. Der Vorgang ist nicht mehr isotherm oder isobar.
5-1: Überhitzung vom Sauggas im Verdampfer
1-2: Verdichtung im Verdichter. Durch Reibungsverluste und Motorenabwärme ist der Vorgang nicht mehr isentrop. Die Enthalpie nimmt stärker zu, es muss mehr Arbeit geleistet werden.
2-3: Der Kältekreis gibt Wärme ab. Durch Druckverluste erfolgt die Zustandsänderung nicht mehr isobar. Druck und Wärmeverluste am Verdichteraustritt (2) (insb. Ventile) und der Heissgasleitung erfordern eine höhere Kompression des Kältemittels um die gewünschte Kondensationstemperatur zu erreichen. Die Heissgasentwärmung (2-2’) ist nicht isobar. Die Kondensation (2’-3) ist nicht isotherm sondern die Kondensationstemperatur nimmt ab. Zwischen 3-3’ wird das flüssige Arbeitsmittel unterkühlt, maximal soweit wie die tiefste Temperatur der Wärmesenke.
3-4: Expansion im Expansionsventil

Manchmal wird über einen Zwischenwärmetauscher das flüssige Arbeitsmittel weiter unterkühlt und damit das Sauggas zusätzlich überhitzt.

Damit ein Wärmestrom fliessen kann, ist immer ein endlich kleiner Temperaturgradient erforderlich. Daher liegt die Verdampfungstemperatur stets unter der Quellentemperatur und die Kondensationstemperatur über jener der Senkenseite (z.B. Heizungswasser).

Wirkungsgrad oder Leistungszahl

Der Wirkungsgrad, besser genannt Leistungszahl, einer Wärmepumpe ist definiert aus dem Quotienten der Wärmeleistung Q_w zur Aufnahmeleistung P_a

Dies gilt sowohl für den verlustfreien als auch den realen Prozess. Die Wärme- und Aufnahmeleistung können jeweils durch die Enthalpiedifferenzen ausgedrückt werden. Für den verlustfreien idealen Wärmepumpenkreisprozesses gilt:

falls die Expansionsarbeit zurückgewonnen werden kann, bzw.

bei isentroper Expansion über eine Drossel (h₃ - h₄ = 0).

Der Wirkungsgrad der realen Wärmepumpe unterscheidet sich in der Formel nur dadurch dass statt h₃, h_3’ auftritt, da durch den Temperaturgradienten im Wärmeträger auf der Warmseite das Kältemittel unterkühlt werden kann. Die Werte der Enthalpien unterscheiden sich jedoch erheblich durch die Verluste.

Den Einfluss der Verluste soll folgendes Beispiel zeigen. Für Quellentemperatur 0°C und Senke 35 °C ist nach Carnot ein maximaler Wirkungsgrad von

möglich.

Der Wirkungsgrad der idealen Wärmepumpe ist vom verwendeten Kältemittel abhängig. Bei der idealen Wärmepumpe ist die Verdampfungstemperatur = Quellentemperatur und Kondensationstemperatur = Senkentemperatur. Die Enthalpien können Tabellen oder Diagrammen entnommen werden. Für das Kältemittel R134a gilt für den genannten Fall:

h₁ = 399 kJ/kg
h₂ = 422 kJ/kg
h₃ = 249 kJ/kg
h₄ = 246 kJ/kg

und damit errechnet sich der Wirkungsgrad zu:

bzw. wenn die Expansion mittels Drossel isenthalp vonstatten geht:

Dieser Wirkungsgrad kann von keiner realen Wärmepumpe mit dem genannten Kältemittel übertroffen und in der Praxis auch nicht erreicht werden.

Die Expansion mittels Drossel führt demzufolge zu einer Einbusse bei der Leistungszahl von etwa 15%.

Wird das Kältemittel nach dem Verdampfen um 5 K überhitzt gilt

h₁ = 403 kJ/kg
h₂ = 427 kJ/kg

Eine Überhitzung hat demzufolge nur marginalen Einfluss auf die Leistungszahl. Allerdings ist eine Überhitzung auf 5°C mit einer Quellentemperatur von 0 °C gar nicht möglich (ausser mit Zwischenwärmetauscher, aber das beachten wir mal nicht). Daher muss die Verdampfungstemperatur 5 K unter der Quellentemperatur liegen. Dann wird die Leistungszahl zu:

In der realen Wärmepumpe haben wir auch keine Wärmequelle mit konstanter Temperatur. Der Wärmeträger verlässt die Wärmepumpe mit tieferer Temperatur als er eintritt. Die Verdampfungstemperatur kann nicht höher sein als die Austrittstemperatur des Wärmeträgers. Zudem muss ein Temperaturgradient zwischen Wärmeträger und Kältemittel bestehen, da sonst keine Wärmeübertragen wird. Daher ist die Annahme von rund 5 K tieferer Verdampfungstemperatur gegenüber der vom Wärmeträger am Verdampfer Eintritt realistisch. Ein weiterer Gradient muss bei der Wärmeabgabe an den Wärmeträger auf der Heizungsseite auftreten. Bei Vorlauf 35 °C und Rücklauf 30 °C ist eine Kondensationstemperatur von 37 °C realistisch. Mit dem kalten Rücklauf kann hingegen das Kältemittel unterkühlt werden. Beachten wir nur mal die für diesen Fall maximal mögliche Unterkühlung von 5 K, dann verbessert sich die Leistungszahl zu

Jedoch wird selten die ganze Unterkühlung genutzt, da auch hier eine Temperaturdifferenz zum Wärmeträger auftreten muss. In unserem Fall wären 32 °C realistisch. Zusammen mit der Kondensationstemperatur von 37 °C folgt dann

Eine weitere Verlustquelle ist der Verdichter. Bei den genannten Betriebsdaten erreichen übliche Verdichter einen COP um 4.2 bis 4.8. Das sind zu den 6.4 immer hin 30-40% weniger, während die 6.4 zu den maximal möglichen 8.8 nur knapp 30% Differenz vorhanden ist. Die meisten Verluste kommen also durch den nicht idealen Verdichter zu stande. Die Verdampfungstemperatur lässt sich noch etwas erhöhen und die Kondensationstemperatur etwas erniedrigen, so dass Wärmepumpen mit COP bis zu 5.0 auf dem Markt zu finden sind. Viel mehr ist aufgrund der schlechten Verdichter auch nicht möglich.